Are you struggling to teach your students to understand distance on the coordinate plane? If so, you’re not alone. One of the key concepts in geometry, distance on the coordinate plane can be challenging for many students to grasp. In this article, we will explore strategies to help your students master distance on the coordinate plane. From breaking down the concept into simpler steps to providing real-life examples and interactive activities, we will cover all the essentials to make this topic more accessible and engaging for your students. By the end of this article, you will have practical ideas and resources that you can immediately implement in your classroom. Whether you’re a teacher looking to enhance your lesson plans or a parent supporting your child’s learning at home, this article will provide you with the guidance you need to ensure your students succeed in mastering distance on the coordinate plane. Get ready to ignite a spark of enthusiasm in your students and make distance on the coordinate plane a breeze!
Encouraging Exploration Before Teaching Distance on the Coordinate Plane
Before teaching students how to find the distance between two points on the coordinate plane, start by reviewing. Begin with how to find the distance between two vertical points and two horizontal points. This review reinforces foundational skills needed to find the distance between two points that are not horizontal or vertical.
Next, have students work in groups to find the distance between two ordered pairs that are not vertical or horizontal. Give students time to explore and use what they know to solve the problem. As they work, circulate the room to observe and listen to their discussions. This is a great opportunity to understand their thought processes.
Once students have had ample time to work, ask each group to share their solutions and reasoning. Some students may discover they can use the Pythagorean Theorem, while others might attempt to estimate the distance. Both approaches offer valuable learning opportunities and spark meaningful discussions.
Use these discussions to guide students toward an essential realization: unlike vertical or horizontal distances, they cannot simply count spaces to measure diagonal distances. Instead, they need a new strategy—one grounded in mathematical reasoning and the principles of geometry.
By engaging students in exploration, discussion, and reflection, you’ll help them build a deeper understanding of how to calculate distances on the coordinate plane.
Teaching Students to Use the Pythagorean Theorem for Distance on the Coordinate Plane
The Pythagorean Theorem is a powerful tool for helping students calculate distances on the coordinate plane. Here’s a step-by-step approach to teach this concept effectively:
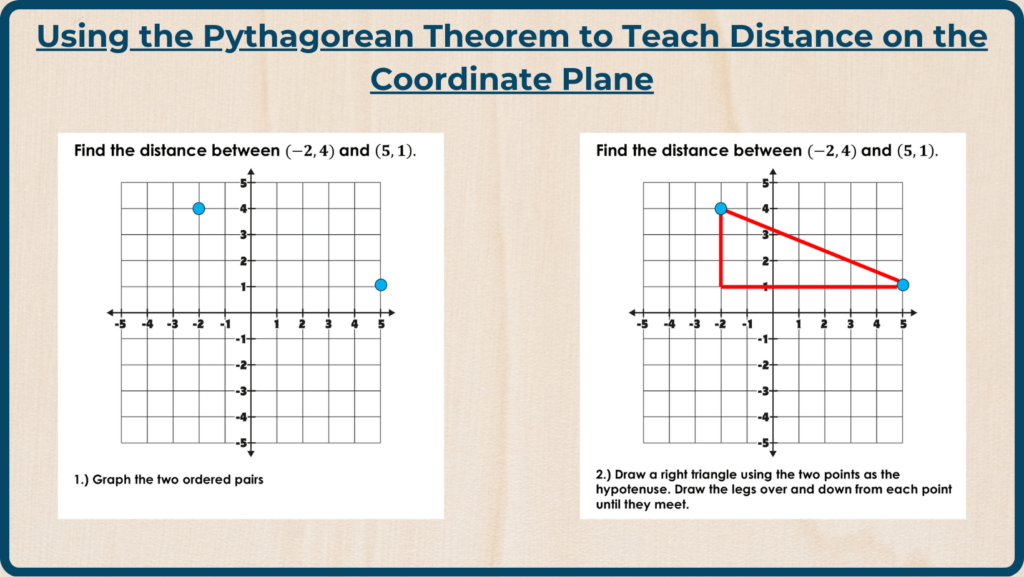
1.) Graph the Points
Begin by having students plot the two ordered pairs on the coordinate plane. This visual representation helps students better understand the relationship between the points.
2.) Draw a Right Triangle
Next, guide students to draw a right triangle by connecting the two points with a diagonal line (the hypotenuse). The vertical and horizontal lines forming the triangle’s legs should extend from the points.
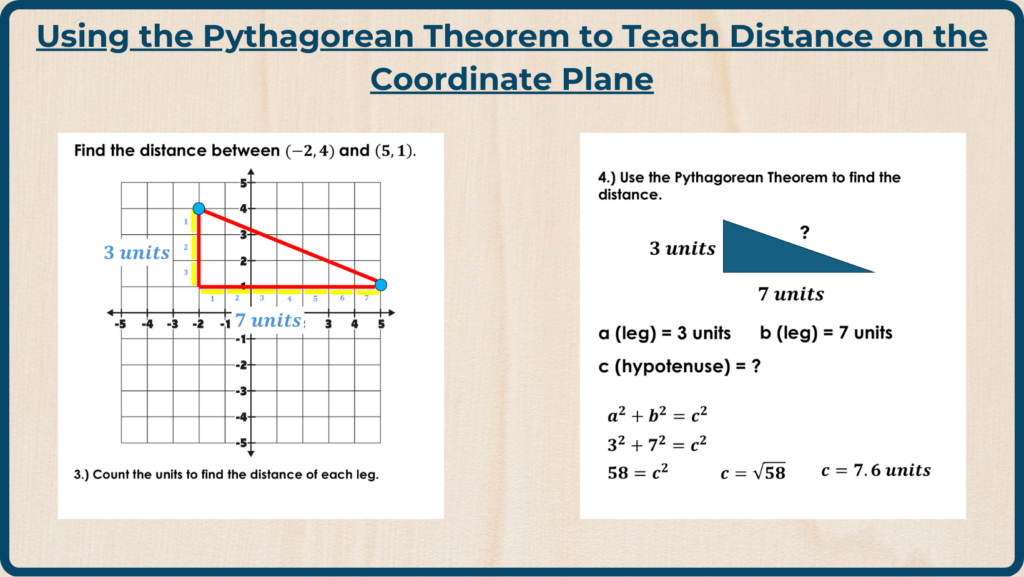
3.) Count the Units
Ask students to count the units along the grid to determine the lengths of the two legs of the triangle.
4.) Apply the Pythagorean Theorem
Use the formula a^2 + b^2 = c^2, where a and b are the lengths of the triangle’s legs, and c is the hypotenuse. This calculation provides the distance between the two points.
5.) Practice and Discover
Provide students with multiple practice problems using this method. Some students will realize they don’t always need to graph the points. By simply looking at the differences in the x-values (horizontal distance) and the y-values (vertical distance), they can find the lengths of the legs mentally.
Encourage this realization, as it lays the groundwork for understanding the distance formula. However, allow students who prefer graphing to continue doing so until they feel confident transitioning to mental calculations. This flexibility ensures all students develop a deeper understanding at their own pace while preparing them for more advanced concepts.
Using The Distance Formula to Find the Distance Between Two Points
When introducing the distance formula to your students, it’s helpful to start with a thought-provoking question: Can you come up with a rule to find the distance between two points? This engages critical thinking and lays the groundwork for understanding.
Once students share their ideas, introduce the distance formula:

Breaking Down the Formula
To make the formula more approachable, break it into its components and visually relate each part to a right triangle:
1.) (x₂ – x₁) represents the horizontal distance (the “run”).
2.) (y₂ – y₁) represents the vertical distance (the “rise”).
3.) Squaring these values ensures all distances are positive and follows the Pythagorean Theorem.
4.) The square root calculates the hypotenuse, which is the distance between the two points.
Use a diagram of a right triangle to connect each part of the formula to the visual representation, helping students see how it all comes together.
Practice and Graphing Tips
Provide practice problems that let students apply the distance formula to different sets of points. For those who struggle, encourage them to plot the points on a graph. Visualizing the points and triangle can clarify the process and build confidence.
With this step-by-step approach, your students will not only learn the distance formula but also understand the logic behind it, ensuring a stronger grasp of the concept.
Check out the resources below on Pythagorean theorem and distance on the coordinate plane.
Conclusion
For most 8th-grade students, the journey to mastering the distance formula begins with drawing right triangles and applying the Pythagorean Theorem. This foundation is invaluable when they progress to Algebra 1 and formally learn the distance formula.
By walking students through this derivation, you emphasize the logic behind the formula rather than presenting it as something to memorize. When students understand that the distance formula is just the Pythagorean Theorem applied to the coordinate plane, they’re more likely to retain it and use it confidently.
This approach not only strengthens their algebra skills but also reinforces the importance of understanding over rote memorization—a valuable lesson for any mathematical concept.
Check out our blog on teaching 8th grade math. Mastering the 8th Grade Math Curriculum.
Click below for a FREE lesson sample from the 8th Grade Transformations unit.